Dowodzenie twierdzeń – czy to się da nauczyć?

Dowodzenie twierdzeń – czy to się da nauczyć?
Cześć z tej strony Arietta – mentor, coach i pasjonat matematyki!
Zapraszam Cię bardzo gorąco do przeczytania artykułu poświęconemu dowodzeniu twierdzeń. Temat trudny, ale myślę, że razem damy radę. Spokojnie nie martw się. W tym artykule będę Cię chciała zabrać do krainy dowód, gdzie czeka na ciebie 5 królestw. Będę Cię chciała po nich oprowadź, wytłumaczyć Ci ich tajemnice i zachęcać, abyś kończąc naukę ze mną mógł samodzielnie spróbować swoich sił w dowodzeniu. Zanim będziemy analizować konkretne zadania i przykłady powiedzmy sobie kilka słów na temat budowy. Zacznijmy zatem od tego, że jeśli w zadaniu zobaczysz sformułowania: “Wykaż, że …”, “Udowodnij, że …”, “Uzasadnij, że …” to znaczy, że jest to zadania do udowodnienia twierdzenia. I teraz twierdzenie z punktu widzenia matematyki składa się z trzech części.
Budowa twierdzenia
Pierwsza część – ZAŁOŻENIE – czyli to co jest dane w zadaniu, konkretnym poleceniu inaczej można by to określić jako dane.
Druga część – TEZA – czyli to co musimy udowodnić, pokazać, uzasadnić.
Trzecia, a zarazem najtrudniejsza część – DOWÓD – czyli ta część którą musimy wykonać sami bo tezę i założenie odnajdziemy w treści zadania. Możemy zatem powiedzieć, że dowód to zbiór czynności jakie musimy wykonać, aby pokazać prawdziwość tezy. I teraz tak, są dwa rodzaje dowodów:
Rodzaje dowodów
- dowód wprost – polega na tym, że wychodzimy z jednej strony tezy np. z lewej i dochodzimy do drugiej czyli w tym momencie prawej strony, wykonując kolejne następujące po sobie przekształcenia.
- dowód nie wprost (Pamiętaj na maturze musisz to zasygnalizować, pisząc np. dowód nie wprost, albo $D^{-1}$). Powiedzmy sobie zatem, na czym polega ten dowód i kiedy go stosować. Otóż w moim odczuciu najlepiej go stosować np. dowodząc nierówności. Ten rodzaj dowodu polega na tym, że my dowodząc w ten tezę zaprzeczamy jej. Czyli np. w tezie mamy: $x>0$ to w dowodzie nie wprost piszemy $x<0$. Następnie dowodzimy daną nierówność dokonując przekształcenia i dochodzimy do sprzeczności co w konsekwencji powoduje prawdziwość tezy.
Takim metodami będziemy teraz dowodzić poniższe twierdzenia. Poniżej znajdują się zadania z lekcji, a pod nimi odnajdziesz link do filmu gdzie krok po kroku będę Ci się starała je objaśnić i nauczyć Cię jak Ty masz spróbować dowieść zadania podobne do tych, które ja przygotowałam.
KROK I – Dowodzenie twierdzeń – równania i nierówności
- Udowodnij, że jeżeli $a$ jest liczbą rzeczywistą różną od zera i $a+ \frac{1}{a}=3$, to $a^2+\frac{1}{a^2}=7$
- Wykaż, że dla każdej liczby rzeczywistej $a$ i każdej liczby rzeczywistej $b$ prawdziwa jest nierówność: $(\frac{a+b}{2})^2 \leq \frac{a^2+b^2}{2}$
- Udowodnij, że dla każdej dodatniej liczby rzeczywistej $x$ prawdziwa jest nierówność: $4x+\frac{1}{x} \geq 4$
- Wykaż, że dla dowolnych liczb rzeczywistych $x$, $y$ prawdziwa jest nierówność: $4x^2+5y^2-4xy \geq 0$
- Uzasadnij, że dla dowolnych liczb rzeczywistych $x$, $y$ prawdziwa jest nierówność: $x^4+y^4+x^2+y^2 \geq 2(x^3+y^3)$
- Wykaż, że dla wszystkich nieujemnych liczb rzeczywistych $x$, $y$ prawdziwa jest nierówność: $x^3+y^3 \geq x^2y+y^2x$
KROK II – Dowodzenie twierdzeń – podzielność
Zanim zajmiemy się tymi rodzajami dowód. Przypomnijmy sobie kilka istotnych informacji dotyczących zapisu algebraicznego liczb o zadanej cesze podzielności. Zastanówmy się zatem co to znaczy, że liczba jest podzielna np. przez 3. To znaczy że gdybym tą liczbę podzieliła pisemnie to z dzielenia pisemnego reszta wynosiłaby zero. Czy np. liczba 6 jest podzielna przez 3 bo da się zapisać w postaci iloczynu liczby 2 razy 3. Weźmy inny przykład, 300 jest podzielne przez 3 bo jest iloczynem liczby 100 i liczby 3. Jeśli pójdziemy dalej to zauważymy, że liczba jest podzielna przez 3 zawsze wtedy gdy da się zapisać w postaci iloczynu liczby 3 i dowolnej liczby całkowitej, którą w dowodach oznaczamy zazwyczaj przez $n$. Zapiszmy zatem kilka przykładów licz o zadanej cesze podzielności
Przykłady liczb z zadaną cechą podzielności
- $x=3 \cdot n, n \in C$ – liczba $x$ jest podzielna przez 3
- $x=7 \cdot n, n \in C$ – liczba $x$ jest podzielna przez 7
- $x=2 \cdot n, n \in C$ – liczba $x$ jest podzielna przez 2, zauważ że w ten właśnie sposób w szkole zapisujemy liczbę parzystą
- $x=2 \cdot n+1, n \in C$ – liczba $x$ jest to przykład liczby nieparzystej, zauważ również, że moglibyśmy o tej liczbie powiedzieć że jest to liczba podzielna przez 2 ale z resztą 1
- $x=3 \cdot n+2, n \in C$ – liczba $x$ jest podzielna przez 3 z resztą dwa, pamiętaj, że liczby podzielne przez 3 są od siebie odległe o 3 więc możesz spotkać również zapis $x=3 \cdot n-1, n \in C$
- $x=7 \cdot n+5, n \in C$ oraz $x=7 \cdot n-2, n \in C$ – liczba $x$ jest podzielna przez 7 z resztą 5
Jeśli wiesz już, jak zapisywać liczby o zadanej cesze podzielności może przejść do oglądania lekcji, którą dla Ciebie przygotowałam. Zapraszam serdecznie.
ZADANIA
- Uzasadnij, że suma kwadratów trzech kolejnych liczb całkowitych przy dzieleniu przez $3$ daje resztę $2$
- Wykaż, że liczba $6^{100}-2 \cdot 6^{99}+10 \cdot 6^{98}$ jest podzielna przez $17$
- Uzasadnij, że dla każdej liczby dodatniej całkowitej $n$ liczba $3^{n+2}-2^{n+2}+3^n-2^n$ jest wielokrotnością liczby $10$
- Uzasadnij, że każda liczba całkowita $k$, która przy dzieleniu przez $7$ daje resztę $2$, ma tę własność, że reszta z dzielenia liczby $3k^2$ przez $7$ jest równa $5$.
- Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych parzystych jest podzielna przez $24$.
- Wykaż, że reszta z dzielenia przez $8$ sumy kwadratów dwóch kolejnych liczb nieparzystych jest równa $2$.
KROK III – Dowodzenie twierdzeń – tożsamości trygonometryczne
Jest to dosyć trudny temat dla przeciętnego ucznia, dlatego ucząc się ze mną musisz zwrócić szczególną uwagę na wzory, które dla Ciebie muszę napisać. Wzory te będziemy nazywali podstawowymi tożsamościami trygonometrycznymi i na nich oprzemy dowodzenie twierdzeń, które odnajdziesz poniżej.
$sin^2x+cos^2x=1$ – “Jedynka trygonometryczna”
$tgx=\frac{sinx}{cosx}$ – pamiętaj, że wzór ten wymaga założenia, że $cosx \neq 0$
$ctgx=\frac{cosx}{sinx}$ – założenie: $sinx \neq 0$$tgx \cdot ctgx=1$, przy założeniu, że: $sinx \neq 0$ i $cosx \neq 0$
Jeśli zatem stworzyliśmy sobie fundament do dowodów tożsamości, to zabierzmy się do rozwiązywania zadań. Zapraszam.
ZADANIA
- Sprawdź, czy podana równość jest tożsamością trygonometryczną: $(sinx+cosx)^2=1+2sinx \cdot cosx$
- Wykaż, że podana równość jest tożsamością trygonometryczną: $(1+sinx) \cdot (\frac{1}{cosx}-tgx)=cosx$
- Sprawdź czy podana równość jest tożsamością trygonometryczną: $\frac{1-ctg^2x}{1+ctg^2x}=1-2cos^2x$
- Sprawdź czy podana równość jest tożsamością trygonometryczną: $\frac{sinx}{1+cosx}+\frac{1+cosx}{sinx}=\frac{2}{sinx}$
KROK IV – Dowodzenie twierdzeń – przystawanie trójkątów
- W trójkątach $ABC$ i $A_1 B_1 C_1$ poprowadzono środkowe $BD$ oraz $B_1 D_1$. Wiedząc, że $|BD|=|B_1 D_1 |$, $|BC|=|B_1 C_1 |$ oraz $|∡DBC|=|∡D_1 B_1 C_1 |$, wykaż, że trójkąt $ABC$ jest przystający do trójkąta $A_1 B_1 C_1$.
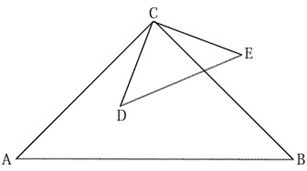
- Trójkąty prostokątne równoramienne $ABC$ i $CDE$ są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku $C$ jest prosty). Wykaż, że $|AD|=|BE|$.
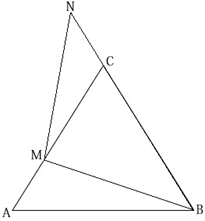
3. Trójkąt $ABC$ przedstawiony na poniższym rysunku jest równoboczny, a punkty $B, C, N$ są współliniowe. Na boku $AC$ wybrano punkt $M$ tak, że $|AM|=|CN|$. Wykaż, że $|BM|=|MN|$.
4. Na bokach trójkąta równobocznego $ABC$ (na zewnątrz tego trójkąta) zbudowano kwadraty $ABDE$, $CBGH$ oraz $ACKL$. Udowodnij, że trójkąt $KGE$ jest równoboczny.
KROK V – Dowodzenie twierdzeń z geometrii na maturze
Matura podstawowa, Maj 2018, zadanie 29
Okręgi o środkach odpowiednio $A$ i $B$ są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku $A$ jest równy $2$. Uzasadnij, że promień okręgu o środku B jest mniejszy $\sqrt{2}-1$
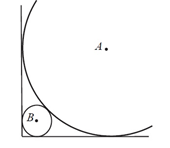
Matura podstawowa, Maj 2018, zadanie 29
Matura podstawowa, Czerwiec 2018, zadanie 29
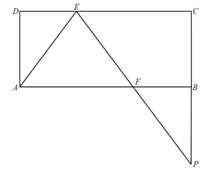
Dany jest prostokąt $ABCD$. Na boku $CD$ tego prostokąta wybrano taki punkt $E$, że $|EC|=2|DE|$, a na boku $AB$ wybrano taki punkt $F$, że $|BF|=|DE|$ . Niech $P$ oznacza punkt przecięcia prostej $EF$ z prostą $BC$ (zobacz rysunek). Wykaż, że trójkąty $AED$ i $FPB$ są przystające.
Matura podstawowa, Maj 2017, zadanie 28
Dane są dwa okręgi o środkach w punktach $P$ i $R$, styczne zewnętrznie w punkcie $C$. Prosta $AB$ jest styczna do obu okręgów odpowiednio w punktach $A$ i $B$ oraz $|∢APC|=α$ i $|∢ABC|=β$ (zobacz rysunek). Wykaż, że $α =180° – 2β$.
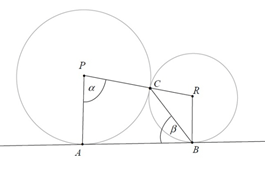
Matura podstawowa, Maj 2017, zadanie 28
Matura podstawowa, Czerwiec 2016, zadanie 29
Dany jest trapez prostokątny $ABCD$ o podstawach $AB$ i $CD$ oraz wysokości $AD$. Dwusieczna kąta $ABC$ przecina ramię $AD$ w punkcie $E$ oraz dwusieczną kąta $BCD$ w punkcie $F$ (zobacz rysunek). Wykaż, że w czworokącie $CDEF$ sumy miar przeciwległych kątów są sobie równe.
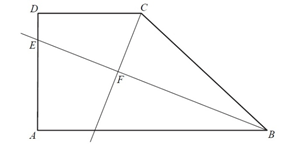
Matura podstawowa, Czerwiec 2016, zadanie 29
Matura podstawowa, Czerwiec 2016, zadanie 29
Dany jest kwadrat $ABCD$. Przekątne $AC$ i $BD$ przecinają się w punkcie $E$. Punkty $K$ i $M$ są środkami odcinków – odpowiednio – $AE$ i $EC$. Punkty $L$ i $N$ leżą na przekątnej $BD$ tak, że$|BL|=1/3 |BE|$ oraz $|DN|=1/3 |DE|$ (zobacz rysunek). Wykaż, że stosunek pola czworokąta $KLMN$ do pola kwadratu $ABCD$ jest równy $1: 3$.
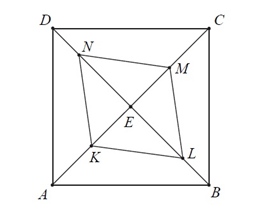
Matura podstawowa, Czerwiec 2016, zadanie 29
Ucz się z AjkaMat.pl
Chcesz nauczyć się więcej, ale nie masz pojęcia od czego zacząć. Potrzebujesz gotowego planu, wg którego zaczniesz krok po kroku się uczyć. Nie chcesz działać po omacku, tracić czasu. Chcesz ruszyć z miejsca, i nie odkładać wszystkiego na później.
Czy powyższe stwierdzenia pasują do Ciebie? To świetnie 🙂 Rozwiązania i metody, które przedstawiam w swoich kursach, bazują wyłącznie na moim wieloletnim doświadczeniu. Wszystko to, o czym mówię zostało przeze mnie przetestowane i sprawdzone podczas pracy z moimi uczniami – nie wierzysz? Sprawdź co mówią o moich lekcjach inni. Odnajdź mnie na YouTube lub Facebooku.
Skorzystaj z mojego doświadczenia, zaufaj mi i ucz się ze mną.




